How to count to 1296 in Ngkolmpu
In order to feed his family for the year, and prove himself a worthy man, a man living in southern New Guinea is expected to grow 1296 yams (dioscorea sp.) each season. In Ngkolmpu, a language spoken by around 200 people who live in this region in a single village 15kms within the Indonesian side of the border between West Papua and Papua New Guinea, there is a single word for this number ntamnao.
To speakers of English, this seems like an arbitrarily specific number; yet to Ngkolmpu speakers it’s perfectly natural. Ngkolmpu, along with most of its related languages, has what is known as a senary numeral system also known as a base-six system. In English, we use a decimal system which is based on recursions of ten units while senary systems are based around recursions of six. In Ngkolmpu, the words for one to six are naempr, yempoka, yuow, eser, tampui and traowow. Seven is naempr traowo naempr or ‘one six and one;’ thirteen is yempoka traowo naempr or ‘two six and one.’ You should be starting to see the pattern now. But what happens when you get to six groups of six, i.e. 62 or 36? Well there is a specific word for that ptae. In fact, in Ngkolmpu there are words for 62, 63, 64 and 65. That’s all the way up to 7776! Related language Komnzo even has a word wi which is used for 66 or 46,656! If you want to learn how to count to 7776 in Ngkolmpu the entire system is presented in Table 1.
| 1 | naempr | |
| 2 | yempoka | |
| 3 | yuow | |
| 4 | eser | |
| 5 | tampui | |
| 6 | 61 | traowo |
| 7 | naempr traowo naempr | |
| 8 | naempr traowo yempoka | |
| 13 | yempoka traowo naempr | |
| 36 | 62 | ptae |
| 216 | 63 | tarumpao |
| 1296 | 64 | ntamnao |
| 7776 | 65 | ulamaeke |
Table 1 – Senary numerals in Ngkolmpu
While we are used to decimal counting systems in English, lots of languages around the world use different systems. What is remarkable is that these senary systems are essentially unique to the southern New Guinea region. As far as we know, the only languages which use base-six are found in this region. In Ndom, a completely unrelated language to Ngkolmpu spoken on Yos Sudarso Island around 250kms away have a sort of light six-base system. Ndom displays unique words for the numbers one to six, but no words higher terms and no way to construct them from lower numerals; this is what is known as a ‘restricted numeral system.’ As far as we know, this complex base-six system as we see in Ngkolmpu and its relatives are an entirely unique development. This then raises a crucial question: How and why did such a system emerge?

This is a hard question to answer. The leading theory on this is based on the primary use of the counting systems: yam tallying. In the communities of southern New Guinea, the various species of dioscorea aka yam are extremely important for every part of life. They are the primary food staple and, as we said before, the general consensus is that it takes a ntamnao of yams to feed a family for a year. Good yam gardeners count their yams to ensure they have enough food for the year but just as importantly for the bragging rights that accompany being a good gardener. Additionally, yams serve many ceremonial roles, for instance a wedding feast can’t be held without a ntamnao of yams which are meticulously counted, brought to the bride’s village and counted again with all parties present. Smaller feasts might require a tarumpao (216) which are counted and distributed to participants as in Picture 2. The significance of counting yams in these cultures has been hypothesised as the motivation for the development this counting system; something we don’t really see anywhere else in the world. The next question is why base six and not some other number? Well, the main yams consumed in this region are teardrop shaped with a round end and a narrow end. These when placed into small piles naturally fall into neat piles of 6 (Picture 3). This provides a motivation for a specifically 6 based system and supports the claim that numeral system emerged through the practice of tallying yams.

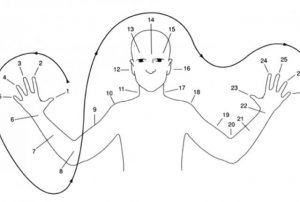
The Ngkolmpu system only has numerals up to 7776 but hypothetically could be used to count to any number. Numeral systems of this type are known as ‘unrestricted numeral systems.’ We take this for granted in English but in smaller communities these are typically not that common. For example, in Marind a culturally dominant language spoken by around 9000 people in the same region as Ngkolmpu have words for one and two only. Counting is done by counting fingers and toes without any productive means for extending beyond that. Similar are the body part tallies of New Guinea such as the Oksapmin body part tally where one can count up to 27 by listing names for the places along the fingers, hands, arms and head for values up to 27 (Picture 4). This is very different to the Ngkolmpu system as we see in Table 1.
It was previously thought that unrestricted numeral systems could only develop in cultures which had sufficient organisational bureaucracy to warrant such a system. What the southern New Guinea situation shows is that the agrarian practices of yam cultivation under certain conditions also allow for the development of advanced counting systems. So, it looks like if people want to count something enough, they can develop the systems to do so which is remarkable.
The next time you have to count up something in multiples of six spare a thought for the Ngkolmpu and their wonderful counting system.
19 thoughts on “How to count to 1296 in Ngkolmpu”
There’s another group who count in sixes, namely cricketers. But it wasn’t always so. At different times and places, an over has had four, five or eight balls. Now six it standard; see https://en.wikipedia.org/wiki/Over_(cricket)
Ah that’s fantastic! Perhaps we could convince the international cricketing body to swap over to the Ngkolmpu counting system for their games…
If they have words up to 6^5 then they can count up to 6^6-1, i.e 46645, which should be 555555 in base 6.
Also, do they know the zero?
Do you know if it would be OK to say, for instance, 36 as ‘naempr ptae’? That would mean it would be regular (not sure if that’s the right term) with, say, ‘naempr ptae naempr’.
And… we count eggs in multiples of six (half a dozen, dozen, etc.), dice have six sides, and dominos have up to six spots. Our clock face also uses sixes and twelves. Also, the Imperial units of length…?
My understanding of our use of dozens is that it is originated with using the tip of the thumb to count the phalanges of the fingers. This gives four fingers with three phalanges on each hand – i.e., a dozen. So it is more likely dozens (for which we also have a name) rather than sixes (for which we don’t) that is the basis of this system.
Likewise perhaps the 60-based systems of Mesopotamia that we still use – we use the five fingers of one hand to enumerate sets of dozens counted off on the other. Hence 60.
Thanks to Alex Bellos for drawing Guardian readers to this. Another simple explanation is that it results from counting the fingers of one hand but not having a zero. So you count to 5 and then put down a stone or a stick or a yam! So you now have yam, yam and 1 finger, yam and 2 fingers etc. then 2 yams and 1 ….. After 5 yams and 5 you maybe put down a bag of yams (or stones or twigs) so you now have “bag” and so for instance 3 bags, 4 yams and 3 fingers. I wonder if traowo means anything else in their language.
HOW TO SAY 1296 IN SENARY